Mathematical constants are cornerstones of many theoretical and applied sciences. From the well-known \(\pi\), the ratio of a circle’s circumference to its diameter, to the enigmatic \(\gamma\), the Euler-Mascheroni constant, these numbers have fascinated mathematicians for centuries. Understanding their properties has led to breakthroughs in geometry, number theory, physics, and engineering. For instance, the discovery of logarithms revolutionized calculations, and the transcendence of \(\pi\) reshaped our understanding of algebraic structures. As we look forward, the deeper exploration of constants — beyond their numerical values — offers immense potential for uncovering new mathematical truths and enhancing computational methods across disciplines.
The relationships between mathematical constants often reveal unexpected beauty and profound truths. One striking example comes from Srinivasa Ramanujan’s groundbreaking work, where he unveiled a deep connection between \(\pi\), \(e\), and continued fractions. The formula expresses \(\sqrt{\pi e / 2}\) as a sum of a continued fraction and an infinite series:
\[ \sqrt{\frac{\pi e}{2}} = \frac{1}{1 + \frac{1}{2 + \frac{1}{3 + \frac{1}{4 + \frac{1}{5 + \cdots}}}}} + 1 + \frac{1}{3} + \frac{1}{15} + \cdots + \frac{1}{(2n-1)!!} + \cdots \]
This intricate relationship highlights Ramanujan’s genius in discovering connections between seemingly unrelated constants through elegant and often surprising formulations.
Inspired by this profound interconnectedness, we set out to create a comprehensive resource: the Ramanujan Library. This database is designed to store an extensive array of mathematical constants, each accompanied by rich metadata, including formulas generating each constant, and, most importantly, the relationships between the constants. By documenting these connections, we aim to provide a tool for researchers to navigate the intricate web of constants and their properties.
For example, another formula for \(\sqrt{\pi e / 2}\) is:
\[ \sqrt{\frac{\pi e}{2}} = \frac{1}{1 + \frac{1}{2 + \frac{1}{3 + \frac{1}{4 + \frac{1}{5 + \cdots}}}}} + 1 + \frac{1/2}{1 + \frac{1/4}{1 + \frac{1/6}{\ddots + \frac{1/(2n)}{1 + \cdots}}}} \]
It was found automatically by the system. In fact, multiple novel relations were found:
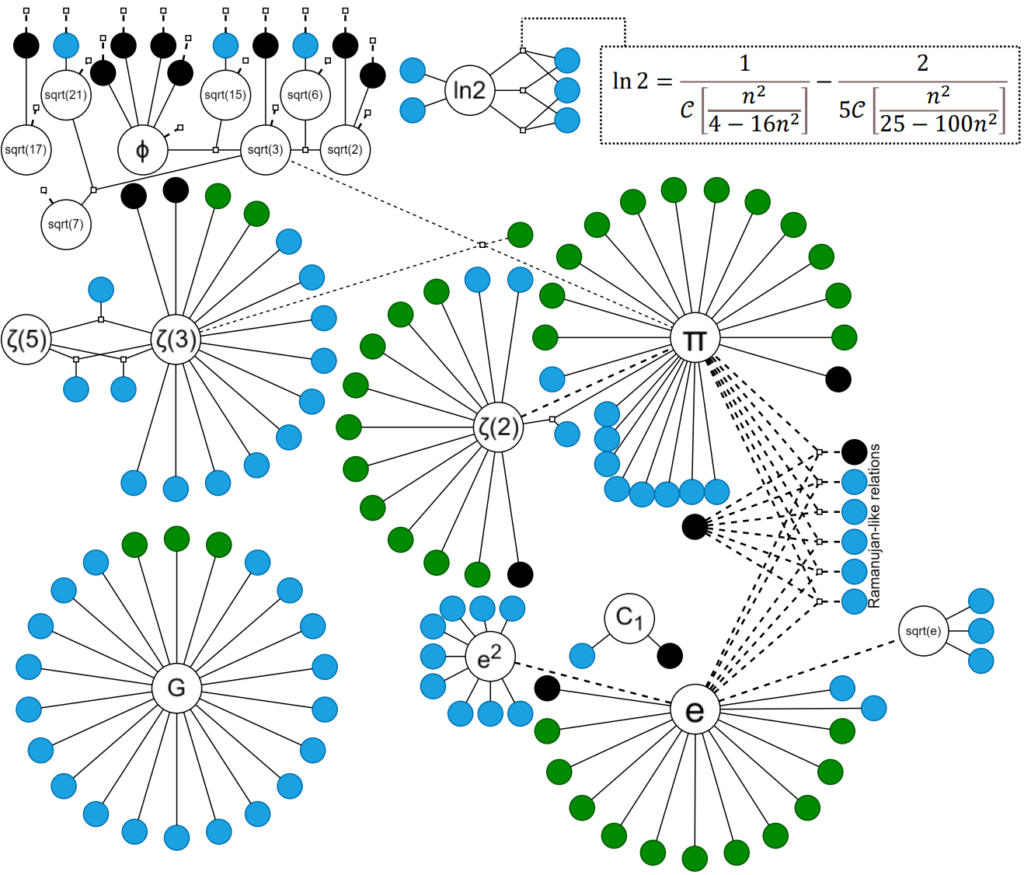
Here each vertex is a constant, and each edge is a formula. Read more in the paper.
We use the PSLQ algorithm and its variants to identify integer relations. To know what precision is sufficient and tell apart a likely result from a false positive, we introduce a return on investment (RoI) measure. This method prioritizes elegance and simplicity.
For example, the number 0.8495652290410995632664106665842862051278871883427131977 is not identified as being related to any known constants by Wolfram Alpha (see for yourself), while the Ramanujan Library correctly identifies it as the first digits of \(\frac{5A + 6B}{5A + 9B}\), where A and B are respectively the first and second Lemniscate constants (see our own tool for identifying and connecting numerical values).
The Ramanujan Library aspires to be more than a repository — it is a dynamic, evolving platform to foster discovery and collaboration in mathematical research. Furthermore, this database has the potential to serve as a training ground for machine-learning models, providing the data for their training. Other works by the Ramanujan Machine collaboration now rely on this resource in algorithms that help detect patterns that complement human intuition (see our publications).
We hope that you will be interested in contributing. New formulas and new constants can be sent to itaybe(at)campus.technion.ac.il – they will be reviewed and added to the library. In the future, advanced users will have permissions to contribute directly and help review other submissions.
Please see the repository for the full implementation.
This research received software engineering support from the Georgia Institute of Technology’s Scientific Software Engineering supported by Schmidt Sciences, as part of the Virtual Institute for Scientific Software (VISS) Program.