This page summarizes results on mathematical constants found by community members, who either contributed computational resources, directly used the Ramanujan Machine algorithms, or developed related methods.
We really appreciate the effort by everyone in the community who contribute to efforts in this growing field of research, and especially thank the following contributions.
John Dalbec and Shahar Gottlieb (March 11th, 2021)
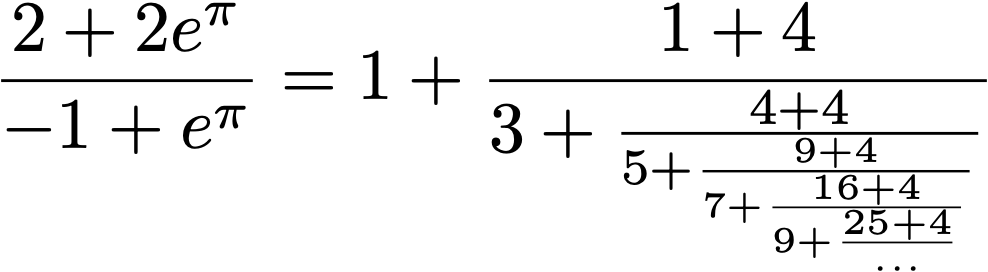
Converges with a rate of 0.75783 digits per term.
Update: On April 12th, 2021, we found an equivalent result in the appendix of the book Continued Fractions: Convergence Theory by Lisa Lorentzen and Haakon Waadeland. The appendix is available here.
Zhu He (June 21st, 2020)
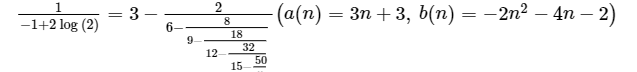
Paul Michalski (July 18th, 2019)
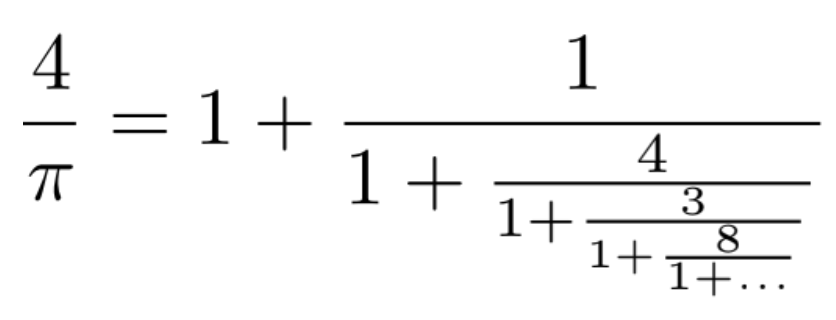
Wolfgang Berndt and Rotem Elimelech (June 2022)
A infinite family of continued fraction for the Hurwitz Zeta Function ![]() , which is related to Apéry’s constant.
, which is related to Apéry’s constant.
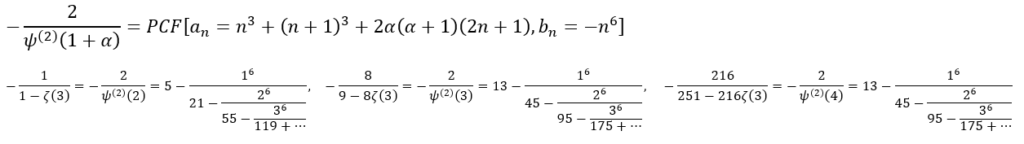
Wolfgang Berndt and Shahar Gottlieb (February 2019)
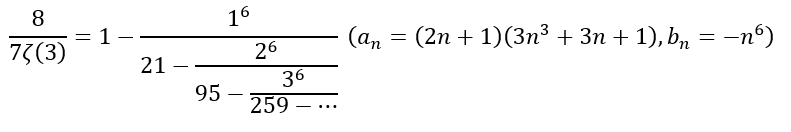
The BOINC Community and the Ramanujan Machine team (June 2022)
The BOINC Community found many results for the fourth order of the Polylogarithm function. These results were used by The Ramanujan Machine team to create an infinite family of continued fractions for any order of the polylogarithm function.
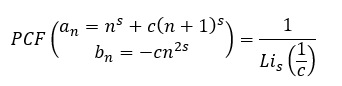
You can see a proof for this general scheme here.
Éric Brier, David Naccache, and Ofer Yifrach-Stav
This team found an infinite family of continued fractions that generalizes many of the results from the first Ramanujan Machine paper. Below is a beautiful example from their work.
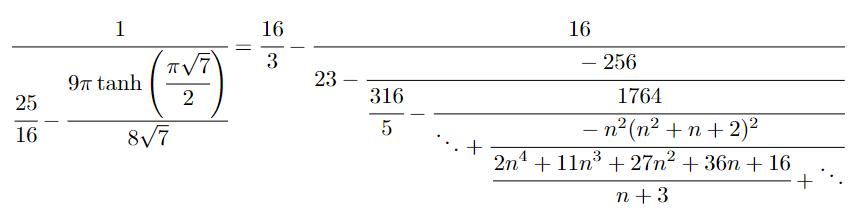
The infinite family of continued fractions they found overlaps with infinite families found by Yahel Manor, Wolfgang Berndt, and others in the Ramanujan Machine team. The representations do not look equivalent but are likely equivalent under some transformation, so we are working to try to sort this out and will update with what we find.