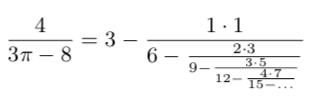
Fundamental constants like e and π are ubiquitous in diverse fields of science, including physics, biology, chemistry, geometry, and abstract mathematics. Nevertheless, for centuries new mathematical formulas relating fundamental constants are scarce and are usually discovered sporadically by mathematical intuition or ingenuity.
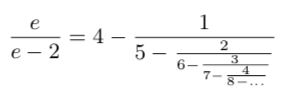
The Ramanujan Machine is a novel way to do mathematics by harnessing your computer power to make new discoveries. The Ramanujan Machine already discovered dozens of new conjectures.
Our algorithms search for new mathematical formulas. The community can suggest proofs for the conjectures or even propose or develop new algorithms. Any new conjecture, proof, or algorithm suggested will be named after you.
We hope that the Ramanujan Machine project will inspire future generations about mathematics and AI-driven science. Please join our mailing list if you would like to get updates on our work.
There is a most profound and beautiful question associated with the observed coupling constant, e – the amplitude for a real electron to emit or absorb a real photon. It is a simple number that has been experimentally determined to be close to 0.08542455. (My physicist friends won’t recognize this number, because they like to remember it as the inverse of its square: about 137.03597 with about an uncertainty of about 2 in the last decimal place. It has been a mystery ever since it was discovered more than fifty years ago, and all good theoretical physicists put this number up on their wall and worry about it.) Immediately you would like to know where this number for a coupling comes from: is it related to pi or perhaps to the base of natural logarithms? Nobody knows. It’s one of the greatest damn mysteries of physics: a magic number that comes to us with no understanding by man. You might say the “hand of God” wrote that number, and “we don’t know how He pushed his pencil.” We know what kind of a dance to do experimentally to measure this number very accurately, but we don’t know what kind of dance to do on the computer to make this number come out, without putting it in secretly!— Richard P. Feynman (1985).
Want to contribute to the Ramanujan Machine?
 |  |  |
| Have no time? Let your computer discover new conjectures whenever you’re not using it. Have a conjecture named after you! | Have time for math? Suggest a proof to any of the conjectures that were discovered by the Ramanujan Machine. Have a formula named after you! | Have time to code? Propose or develop new algorithms to explore new mathematical structures. Have an algorithm named after you! |
